Prioritized Experience Replay (DQN) - 强化学习笔记

arXiv原文：https://arxiv.org/abs/1511.05952

最近为了做课程项目看了几篇DQN相关的论文，主要都是基于DQN做一些优化的，Prioritized Experience Replay (PER) 就是其中之一。PER是针对经验回放池 (Experience Replay, EP) 做的优化，思路也很简单：不同于DQN中的随机采样，而是按照经验的重要性进行采样，越是重要的样本被采样的概率就越高，从而充分利用样本的信息，加快网络的训练过程。

动机

在论文中，作者举了一个Blind Cliffwalk的例子。假如一个agent在每一个step可以有两个action选择：向左走和向右走，如果选择了错误的action，就将掉下悬崖，导致episode终止。这就意味着，agent必须在一个episode中的每一步都能采取正确的action才能最终获得reward，如下图所示，这就导致在EP中需要大量的样本来让agent进行训练。这有点像鱿鱼游戏的第五关，在过玻璃桥时有两个选择，要么踩在强化玻璃上，要么踩在普通玻璃上，也就是会掉下去。前面的人基本没有过关的希望，只有死掉了足够多的人，有了足够多的学习样本，后面的人才能通过之前的经验学习到正确的路径。

对于agent来说，那些能获得reward的经验必然是更重要的，这样能给agent一个正向的反馈，朝着我们希望的方向进行学习，很自然地就想到，在EP中按照重要性将经验进行排序，再根据重要性来进行采样，这也就是这篇paper的中心思想。

优先级的表示

用什么来衡量样本的重要性呢？一个合理的方法是通过TD error $\delta$ 来作为样本重要性的估计，因为它的值代表了这个样本有多出乎网络的预料，因此会对训练更有帮助。为了在随机采样和按重要性采样中进行平衡，采用以下的概率来对EP中的样本进行采样： $$ P(i) = \frac{p_i^\alpha}{\sum_kp_k^\alpha} $$ 其中，$p_i$是transition $i$的优先级，$\alpha$是一个用于调节随机采样和按重要性采样的一个参数，如果将$\alpha$取为0，那么此时就等同于随机采样。在表示$p_i$时，有两种方法：

• proportional prioritization: $p_i = |\delta_i|+\epsilon$，$|\delta_i|$为样本$i$的TD error的绝对值，$\epsilon$为一个很小的常量正数，这是为了保证$p_i$不会出现为0的情况；
• rank-based prioritization: $p_i = \frac{1}{rank(i)}$，其中$rank(i)$是transition $i$在EP中按照TD error进行从大到小排序后的排名，这里应该是依据了Zipf’s law。

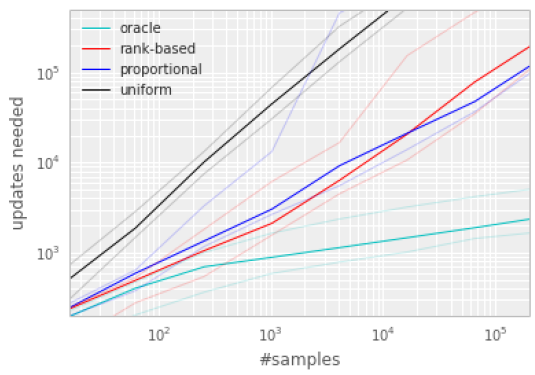
这两种对优先级的表示都是随TD error单调递增的，并且都能有效地加速网络的训练，如下图所示，但是rank-based的表示方法可能会更鲁棒一些。

算法及具体实现

整个算法的流程如下图。

在新存入一个transition时，由于还没有TD error信息，所以给其分配目前最大的优先级，这是为了保证每个transition至少能有机会被采样一次。

为了能高效地进行采样，采样的时间复杂度应当尽可能小，假如EP里总共存了$N$个transition，采样所需要的时间不应该依赖于$N$的大小。为了满足这一需求，针对两种表示，论文提出了两种实现的方案。

Proportional-based的实现

Proportional-based采用了一种叫做sum tree的数据结构，他是一种用数组表示的满二叉树。在叶子节点中存储了真正的信息，其他的每个中间的节点，都保存了每个孩子节点的和，因此根节点保存了所有叶子节点的和。采用这一数据结构的目的主要是为了减小采样的时间复杂度。

为了理解sum tree是如何减小时间复杂度的，我们先看一个普通的采样过程。假如现在我们用一个数组存储了5个样本的优先数，分别是1，7，3，5，6，如下图所示。

现在，我需要按照他们的优先数进行采样。节点$a$被采样的概率为$\frac{1}{1+7+3+5+6}$，节点$b$被采样的概率为$\frac{7}{1+7+3+5+6}$，以此类推。我们可以先计算出这5个节点优先数的总和为$1+7+3+5+6=22$，现在我们从$0-22$随机采样。假如我现在采样到了数字$10$，我就从头与每一个节点的优先数进行对比。首先是节点$a$，$10$比$1$大，因此跳过节点$a$，用$10-1$得到$9$，再将$9$与节点$b$进行对比。同样，$9$比$7$大，因此跳过节点$b$，用$9-7$得到$2$后，再与下一个节点$c$进行对比。$2$比$3$小，因此节点$c$就是我们本次采样的样本。这样，我们可以保证优先数大的节点一定有更高的概率得到采样，而优先数小的节点则具有更小的概率。